Représentation binaire des nombres
Comme introduit dans le chapitre précédent toutes les données ne sont représentées qu'avec des bits (des 0 et des 1) sur la machine. Pour chaque type primitif, un certain nombre de bits est utilisé pour représenter les différentes valeurs possibles pour ce type. On a vu tout ça dans le premier chapitre, rappelez-vous en particulier la figure 5 à la section 1.2.
Par exemple, les byte sont représentés sur 8 bits. Il y a deux possibilités pour le premier bit : 0 ou 1, deux possibilités pour le bit suivant, etc. Cela fait un nombre total de possibilités de $2^8 = 2 \times 2 \times ... \times 2 = 256$ données différentes représentables. Ceci correspond bien à l'intervalle présenté sur la figure 5 : les valeurs qu'on peut représenter avec un byte sont comprises entre -128 et 127, soit 256 valeurs différentes.
Représentation binaire des entiers
En Java, les nombres entiers sont représentés selon la représentation en complément à deux. Les nombres entiers positifs sont représentés en binaire, c'est-à-dire sous forme d'une somme de puissances de deux. Prenons par exemple le nombre binaire présenté sur la figure 23.

À chaque bit est associé une position (les chiffres en petit au-dessus). Le bit en position 0 est appelé bit le moins significatif (LSB, Least Significant Bit) et celui avec la position la plus grande est appelé bit le plus significatif (MSB, Most Significant Bit). Celui-ci vaut toujours 0 pour les nombres positifs.
Comme on le verra par la suite, pour les nombres négatifs, il vaut toujours 1. La première chose à faire lorsqu'on veut connaitre la valeur entière représentée par un nombre binaire est donc de consulter la valeur du bit le plus significatif.
Pour un nombre positif, on obtient sa valeur grâce à la somme de puissances de deux suivante :
$$\sum_{i = 0}^{n - 2} {b_i \times 2^i} \quad = \quad b_0 \times 2^0 + b_1 \times 2^1 + ... + b_{n - 2} \times 2^{n - 2},$$où $n$ représente le nombre total de bits et $b_i$ représente la valeur du bit en position $i$. La valeur du nombre binaire présenté à la figure 23 est donc :
$${\bf 1} \cdot 2^6 + {\bf 0} \cdot 2^5 + {\bf 1} \cdot 2^4 + {\bf 1} \cdot 2^3 + {\bf 1} \cdot 2^2 + {\bf 0} \cdot 2^1 + {\bf 1} \cdot 2^0 = 64 + 16 + 8 + 4 + 1 = 93.$$Nombre entier négatif
Voyons maintenant comment procéder pour trouver la valeur d'un nombre négatif. La figure 24 montre la représentation d'un nombre. On reconnait qu'il s'agit d'un négatif grâce à son son bit le plus significatif qui vaut 1.

Pour retrouver la valeur d'un nombre négatif, il faut procéder en deux étapes. La première consiste à retrouver le complément à deux du nombre; ce complément correspond toujours à un nombre positif. On peut ensuite retrouver sa valeur du nombre en calculant la somme vue précédemment; le nombre ainsi obtenu correspond à l'opposé du nombre qu'on cherche.
La première étape correspond donc à retrouver le complément à deux. La figure 25 illustre la procédure à suivre sur notre exemple. Il suffit de parcourir la représentation binaire en partant du bit le moins significatif vers le plus significatif. On recopie tous les bits jusqu'à rencontrer un 1. Ensuite, on recopie ce 1 et pour tous les bits restants, on les recopie en les inversant : pour les 1 on note donc 0 et inversement.
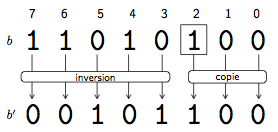
On obtient donc le nombre 00101100. Finalement, le nombre représenté par la représentation binaire $b$ est donné par la somme suivante :
où $b'$ correspond au complément à deux de $b$, calculé par la procédure qu'on vient de décrire. Pour notre exemple, on trouve donc : $-(2^5 + 2^3 + 2^2) = -(32 + 8 + 4) = -44$. Et donc, 11010100 représente le nombre négatif $-44$.
Trouver la représentation d'un nombre
Voyons maintenant comment trouver la représentation binaire d'un nombre entier. Si on note par $n$ le nombre de bits utilisés, il faut que le nombre soit compris entre $-2^{n - 1}$ et $2^{n - 1} - 1$. Par exemple, sur 8 bits, on peut représenter les nombres compris entre $-2^7 = -128$ et $2^7-1 = 127$.
Commençons par les nombres positifs. La technique à utiliser consiste à réaliser des divisions successives par 2 en notant à chaque étape si le reste vaut 0 ou 1. Prenons par exemple la valeur 117 et cherchons sa représentation sur 8 bits. On part donc de 117 qu'on va diviser par deux ce qui donne 58 avec un reste de 1 puisque $117 = 58 \times 2 + 1$ :

On répète ensuite le calcul jusqu'à atteindre 0. La figure 26 montre le calcul complet. La représentation binaire est obtenue en lisant la liste des restes en partant du bas vers le haut. On complète ensuite en mettant les bits les plus significatifs à zéro pour atteindre le nombre de bits requis. Ici, on voulait la représentation sur 8 bits, il faut donc juste ajouter un bit à zéro pour obtenir le résultat qui est 01110101. On peut vérifier que calcul a été correctement effectué : $2^6 + 2^5 + 2^4 + 2^2 + 2^0 = 64 + 32 + 16 + 4 + 1 = 117$.
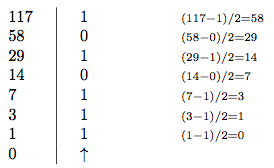
Pour les nombres négatifs, la procédure est similaire. On commence par trouver la représentation du nombre positif correspondant à l'aide de la technique qu'on vient de voir. Ensuite, il suffit de calculer le complément à deux (figure 25) et on obtient ainsi la représentation binaire.
Voyons par exemple comment obtenir la représentation de -117. Il faut commencer par trouver celle de 117 et on l'a déjà fait plus haut, il s'agit de 01110101. On calcule ensuite le complément à deux, c'est-à-dire qu'on parcoure le nombre en partant du bit le moins significatif. On recopie tous les bits jusqu'à tomber sur un 1 qu'on recopie. Tous les bits suivants sont inversés. On obtient donc la solution qui est 10001011.
On verra comment obtenir la représentation binaire d'un entier en Java au chapitre 4. Pour obtenir la valeur d'un nombre binaire, il suffit d'utiliser les littéraux binaires. On peut écrire les instructions suivantes qui reprennent les deux exemples des figures 23 et 24 :
La conversion explicite vers le type byte est nécessaire pour le second nombre, car la conversion par le compilateur n'a pas réussi. L'explication est que les littéraux binaires sont des entiers int et que la séquence 0b11010100 est donc complétée à gauche avec 24 zéros. Le nombre entier correspondant est donc 212, ce qui dépasse le plus grand byte représentable qui est 127, pour rappel.
Opérateur de manipulation de bits
Java propose des opérateurs qui permettent de manipuler directement les bits d'un nombre. Ces opérateurs ne sont applicables que sur sur des entiers et ont pour résultat des entiers. Il y a en tout sept opérateurs de manipulation de bits repris sur la figure 27.
| Opérateur | Description | Exemple | |
|---|---|---|---|
| unaire | ~ |
NON binaire | ~x |
| binaire | & |
ET binaire | x & y |
| |
OU binaire (inclusif) | x | y |
|
^ |
OU binaire (exclusif) | x ^ y |
|
<< |
décalage à gauche | x << y |
|
>> |
décalage à droite (signé) | x >> y |
|
>>> |
décalage à droite (non signé) | x >>> y |
Il y a un opérateur unaire et six binaires. De plus, ceux-ci peuvent se classer en deux catégories qu'on va voir tout de suite : les opérateurs bit-à-bit et ceux de décalage.
Opérateur bit-à-bit
Les opérateurs bit-à-bit ( ~, &, | et ^ ) permettent d'agir sur les bits de leurs opérandes en les prenant deux-à-deux. Ils correspondent aux quatre opérateurs logiques qu'on a vu précédemment. Il suffit de faire la correspondance entre true et 1 et entre false et 0. La figure 28 montre les résultats calculés par ces opérateurs.
x |
y |
~x |
x & y |
x | y |
x ^ y |
|---|---|---|---|---|---|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
Le NON binaire ( ~ ). Il s'agit d'un opérateur unaire qui va inverser tous les bits de son opérande (mettre un 0 quand il y avait un 1 et inversement). Notez que cette opération est également appelée complément à 1. Le ET binaire ( & ) résulte en un 1 si les deux bits sont des 1 et un 0 sinon. Enfin, il reste deux versions du OU binaire. Le OU inclusif ( | ) résulte en un 1 si au moins un des deux bits vaut 1 et un 0 sinon; tandis que le OU exclusif ( ^ ) résulte en un 1 si seulement l'un des deux bit vaut 1 et un 0 sinon. Voici un exemple de programme utilisant ces opérateurs :
La figure 29 montre le résultat calculé par ces différents opérateurs. Pour chaque exemple, vous pouvez voir la représentation binaire sur 8 bits puisqu'il s'agit de données de type byte.
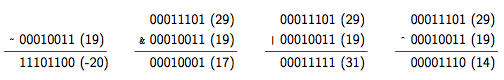
Les opérandes de ces opérateurs doivent être des nombres entiers (ou char). Chacun de ces opérateurs existe en deux versions : le résultat de la première sera de type int et celui de la seconde sera de type long. Les trois opérateurs binaires peuvent être utilisés pour former une affectation composée comme le montre l'exemple suivant :
Opérateur de décalage
Les opérateurs de décalage ( <<, >> et >>> ) permettent de décaler les bits d'un entier d'un certain nombre de positions vers la gauche ou vers la droite. Il s'agit d'un décalage et non d'une rotation; c'est-à-dire que les bits les plus à droite ou à gauche sont perdus lors du décalage. Ces trois opérateurs sont binaires, l'opérande de droite correspondant au nombre de positions de décalage.
La figure 30 montre des exemples utilisant ces opérateurs. Regardons d'abord l'exemple en haut à gauche. Il s'agit d'un décalage à gauche ( << ). Lors du décalage, les bits les moins significatifs du résultat sont complétés par des zéros. Regardons maintenant les deux exemples de droite. Il s'agit d'un décalage à droite ( >> ). Lors du décalage, les bits les plus significatifs du résultat correspondent au bit le plus significatif de l'opérande de gauche. Il s'agit donc d'un décalage signé puisque le signe du résultat sera le même que celui de l'opérande de gauche. Il est également possible d'avoir un décalage à droite non signé ( >>> ) avec lequel les bits les plus significatifs du résultat sont toujours remplis par des zéros.
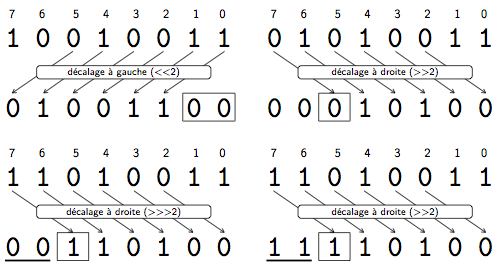
Pour ces trois opérateurs, chaque opérande est converti séparément. Les byte, short et char sont convertis en int et les int et long demeurent inchangés. Le type du résultat de l'opération est int si l'opérande de gauche est un byte, short, char ou int et long si l'opérande de gauche est de type long. Le type de l'opérande de droite ne joue aucun rôle dans la détermination du type du résultat. Enfin, la valeur de l'opérande de droite est d'abord ramenée entre 0 et $n - 1$, où $n$ indique le nombre de bits du type du résultat de l'opération.
Enfin, la valeur de l'opérande de droite est d'abord ramenée entre 0 et $n - 1$ (avec $n$ le nombre de bits du type du résultat). L'exemple suivant décale les bits d'un int (32 bits), de 2, 34 et 66 positions vers la gauche. Elles produisent toute le même résultat, à savoir 20 :
Une propriété intéressante est qu'un décalage sur la gauche de $p$ positions correspond à une multiplication par $2^p$. C'est pourquoi le décalage de 2 positions de l'exemple a provoqué une multiplication par $2^2 = 4$. De manière similaire, le décalage à droite correspond à des divisions de multiples de 2.
Opérateur bit-à-bit comme opérateur booléen
Les opérateurs bit-à-bit ( &, | et ^ ) peuvent être utilisés avec deux opérandes booléens. Dans ce cas, le résultat calculé sera de type boolean. On a déjà vu l'utilisation de ^ et en ce qui concerne les opérateurs & et |, ils fonctionnent comme && et ||. La différence entre les opérateurs binaires et logiques est que ces derniers ne possèdent pas la propriété de court-circuit, c'est-à-dire que les deux opérandes sont toujours systématiquement évalués. Voyons un exemple avec & et && :
La première instruction va produire une erreur d'exécution (division par 0) si la variable x vaut 0 puisque les deux opérandes de & sont toujours évalués. Par contre, la seconde instruction ne produira jamais d'erreur puisque si la variable x vaut 0, le second opérande ne sera pas évalué grâce à la propriété de court-circuit.
Conversion
On peut maintenant comprendre plus facilement les conversions de nombres entiers. Lors de conversions sans perte d'information d'un type entier sur $n$ bits vers un autre type entier sur $n'$ bits (avec $n < n'$), le nombre est étendu avec son bit le plus significatif. Ainsi, 00101100 (byte) deviendra 0000000000101100 (short) et 11010010 (byte) deviendra 1111111111010010 (short). En effet, lors d'une telle conversion, le signe doit être préservé. Lorsque la conversion a lieu vers le type char, le nombre est toujours complété avec des 0 puisque les char ne sont pas signés et correspondent toujours à une valeur positive.
En ce qui concerne les conversions avec perte d'information, si on passe d'un type entier sur $n$ bits vers un autre type entier sur $n'$ bits (avec $n > n'$), le nombre est tronqué; c'est-à-dire que seuls les $n'$ bits les moins significatifs sont conservés (ceux de position $0, 1, ..., n'-1$). La figure 31 montre une telle conversion. On y passe de l'entier int 292 vers le type byte. Vous voyez que de l'information a été perdue : le nombre représenté n'est plus le même !
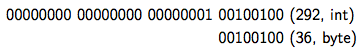
Stocker plusieurs données booléennes
Terminons ce chapitre en voyant un exemple pratique d'utilisation des opérateurs de manipulation de bits. Supposons qu'on ait besoin de huit booléens dans un programme. Une solution consiste à déclarer huit variable de type boolean. Une autre solution consiste à utiliser une seule variable de type byte et d'utiliser chacun de ses bits comme un booléen. Prenons un exemple pour comprendre :
La première instruction déclare une nouvelle variable b de type byte qu'on initialise à 82, dont la représentation binaire est 01010010. Dans la seconde instruction, on part du littéral 1 qui est de type int et on lui fait subir un décalage de trois positions vers la gauche.
La valeur obtenue est 00000000 00000000 00000000 00001000. On se retrouve donc avec un nombre binaire composé uniquement de 0 sauf en troisième position où il y a un 1. La valeur correspondante est 8; on aurait pu directement écrire b |= 8, mais cela aurait rendu le code moins explicite.
On va ensuite appliquer l'opérateur OU binaire entre cette valeur et la variable b. Tous les bits de b vont être conservés sauf celui en troisième position qui valait 0 et qui devient un 1. On répète ensuite l'opération mais en décalant cette fois-ci un 1 de six positions. Tous les bits de b vont être conservés et le 1 qui se trouvait en sixième position reste simplement 1. La figure 32 montre deux exemples dans lequel on force un 1 à une position précise. On voit bien que cette technique fonctionne quelle que soit la valeur qui se trouvait à cette position.

byte.Voyons maintenant comment faire pour forcer un zéro à une certaine position. L'exemple suivant va forcer un zéro à la quatrième position et ensuite à la troisième. Pour ce faire, on part de nouveau du littéral 1 qu'on décale d'autant de positions qu'on souhaite vers la gauche. On va ensuite inverser les 0 et les 1 avec un NON binaire. Pour la première instruction, on obtient donc le nombre 11111111 11111111 11111111 11101111, avec des 1 partout sauf en quatrième position où on a un zéro.
Enfin, on applique un ET binaire entre cette valeur obtenue et la variable b. Le ET binaire permet de conserver tous les bits de b, mais en forçant un 0 à la position voulue.
La figure 33 montre deux exemples dans lequel on force un 0 à une position précise. Encore une fois, cette technique fonctionne quelle que soit la valeur qui se trouvait à cette position.
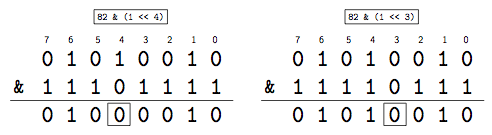
byte.