Triangle de Pascal
Le triangle de Pascal donne les nombres $C_n^k$. Les deux bords du triangle sont constitués de $1$ et chaque cellule contient la somme des deux cellules se trouvant au-dessus. La $k$e valeur se trouvant à la $n$e ligne est $C_n^k$ (on commence à compter avec $0$, la première valeur de la première ligne étant donc $C_0^0$).
Ce triangle recèle de mystère. Les nombres que l'on peut lire correspondent aux puissances de $11$ et si l'on fait la somme des nombres de chaque ligne, on obtient les puissances de $2$ :
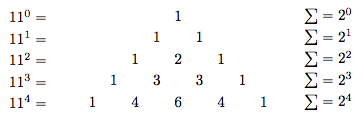
De ce triangle de Pascal, on obtient des propriétés sur les nombres $C_n^k$ :
- Pour tout $n \in \mathbb{N}$, on a $C_n^0 = 1 = C_n^n$.
- Pour tout $n \in \mathbb{N}_0$, on a $C_n^1 = n = C_n^{n - 1}$.
- Pour tout $n, k \in \mathbb{N}_0$, on a $C_n^k = C_n^{n - k}$.
- Pour tout $n, k \in \mathbb{N}_0$, on a $C_n^k = C_{n - 1}^k + C_{n - 1}^{k - 1}$.
Binôme de Newton
Le triangle de Pascal donne également les coefficients du développement du binôme de Newton $(x + y)^n$. La formule de Newton est :
$$\begin{array}{rcl} (x + y)^n & = & C_n^0 x^n + C_n^1 x^{n-1} y + \cdots + C_n^k x^{n-k} y^k + \cdots + C_n^n y^n \;; \\[2mm] & = & \displaystyle\sum_{k = 0}^n C_n^k x^{n-k} y^k. \end{array}$$Par exemple, pour $n = 3$ et $n = 4$, on a :
$$(x + y)^3 = x^3 + 3x^2y + 3xy^2 + y^3.$$ $$(x + y)^4 = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4.$$