Droite des réels
L'ensemble des nombres réels se note $\mathbb{R}$. Un nombre réel est soit un nombre entier (naturel ou relatif), un nombre rationnel ou un nombre irrationnel. Un nombre irrationnel est un nombre qui n'est pas rationnel et s'écrit comme un décimal illimité non périodique; l'ensemble de ces nombres est noté $\mathbb{I}$.
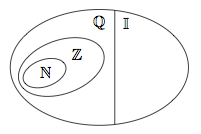
Quelques exemples de nombres faisant partie de ces ensembles :
- $\mathbb{N}$ : $0$, $1$, $2$, $3$...
- $\mathbb{Z}$ : ...$-2$, $-1$, $0$, $1$, $2$...
- $\mathbb{Q}$ : $-\frac{3}{4}$, $0.12$, $-1.666$, $2.837837...$
- $\mathbb{I}$ : $\pi$, $\sqrt{2}$, $e$...
On peut identifier les propriétés suivantes sur ces ensembles :
- $\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}$ et $\mathbb{I} \subset \mathbb{R}$ ;
- $\mathbb{Q} \cap \mathbb{I} = \emptyset$ et $\mathbb{Q} \cup \mathbb{I} = \mathbb{R}$.
Si on place sur une droite deux points que l'on nomme $0$ et $1$, tous les nombres réels peuvent alors s'y placer de façon naturelle. La droite se prolonge sans limite des deux côtés.
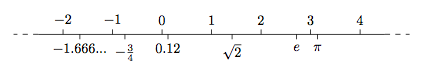
Tout réel admet une écriture décimale soit limitée, soit illimitée. Nous utilisons le point décimal dans ce livre, fréquent dans la littérature scientifique internationale et technique.
Ensemble et intervalle
On peut définir un ensemble de nombres de plusieurs manières différentes. Une définition en extension donne la liste de ses éléments entre accolades, comme par exemple :
$$A = \{ 1, 2, 3, 4, 5, 6 \} \qquad\textrm{ou}\qquad \mathbb{N} = \{ 0, 1, 2, 3... \}.$$Une définition en compréhension donne une propriété qui caractérise ses éléments, définie à droite du symbole $\mid$, comme par exemple :
$$\mathbb{R}_0^+ = \{ x \in \mathbb{R} \mid x > 0 \}.$$On peut également définir un ensemble de nombres réels par un intervalle, correspondant à une demi-droite ou à un segment de droite sur la droite des réels :
| $]a, b[$ | $\{ x \in \mathbb{R} \mid a < x < b \}$ | intervalle ouvert borné |
| $[a, b]$ | $\{ x \in \mathbb{R} \mid a \leq x \leq b \}$ | intervalle fermé borné |
| $]a, b]$ | $\{ x \in \mathbb{R} \mid a < x \leq b \}$ | intervalle semi-ouvert à gauche borné |
| $[a, b[$ | $\{ x \in \mathbb{R} \mid a \leq x < b \}$ | intervalle semi-ouvert à droite borné |
| $[a, +\infty[$ | $\{ x \in \mathbb{R} \mid a \leq x \}$ | intervalle non borné |
| $]a, +\infty[$ | $\{ x \in \mathbb{R} \mid a < x \}$ | intervalle ouvert non borné |
| $]-\infty, b]$ | $\{ x \in \mathbb{R} \mid x \leq b \}$ | intervalle non borné |
| $]-\infty, b[$ | $\{ x \in \mathbb{R} \mid x < b \}$ | intervalle ouvert non borné |
| $]-\infty, +\infty[$ | $\mathbb{R}$ | ensemble des réels |
La longueur des intervalles bornés est $b - a$ et les intervalles non bornés sont de longueur infinie. Un voisinage ouvert d'un nombre réel $x \in \mathbb{R}$ est un intervalle ouvert $]a, b[$ auquel $x$ appartient, c'est-à-dire $a < x < b$.
Inégalité et valeur absolue
Voici plusieurs propriétés sur les inégalités et les valeurs absolues :
- Soient $a, b, c \in \mathbb{R}$. On a : $$\begin{array}[b]{l} a < b \iff a + c < b + c \,; \\ a \leq b \iff a + c \leq b + c. \end{array}$$
- Soient $a, b \in \mathbb{R}$ et $c \in \mathbb{R}_0$. On a : $$\begin{array}[b]{ll} \textrm{si } c > 0, \textrm{alors} & a < b \iff ac < bc \,; \\ & a \leq b \iff ac \leq bc \,, \\ \textrm{si } c < 0, \textrm{alors} & a < b \iff ac > bc \,; \\ & a \leq b \iff ac \geq bc. \\ \end{array}$$
- Soient $a, b, c \in \mathbb{R}$. On a : $$\begin{array}[b]{l} a < b \textrm{ et } b < c \implies a < c \,; \\ a < b \textrm{ et } b \leq c \implies a < c \,; \\ a \leq b \textrm{ et } b \leq c \implies a \leq c. \end{array}$$
- Soient $a, b, c, d \in \mathbb{R}$. On a : $$a < b \textrm{ et } c < d \implies a + c < b + d.$$
- Soient $a, b, c, d \in \mathbb{R}_0^+$. On a : $$a < b \textrm{ et } c < d \implies ac < bd.$$
- Soient $a, b \in \mathbb{R}$. On a : $$\begin{array}[b]{l} 0 < a < b \implies a^2 < b^2 \,; \\ a < b < 0 \implies a^2 > b^2. \end{array}$$
- Soient $a, b \in \mathbb{R}_0$. On a : $$\begin{array}[b]{l} \displaystyle 0 < a < b \textrm{ ou } a < b < 0 \implies \frac{1}{a} > \frac{1}{b} \,; \\[4mm] \displaystyle a < 0 < b \implies \frac{1}{a} < \frac{1}{b}. \end{array}$$
- Soit $a \in \mathbb{R}_0^+$. On a : $$|x| \leq a \iff -a \leq x \leq a.$$
- Soit $a \in \mathbb{R}$. On a : $$-|a| \leq a \leq |a|.$$
- Soient $a, b \in \mathbb{R}$. On a : $$|a + b| \leq |a| + |b|.$$
Élément particulier de $\mathbb{R}$
On retrouve des éléments particuliers dans $\mathbb{R}$, si on considère l'ensemble des réels ordonnés par la relation d'ordre $\leq$ et une partie $P$ de $\mathbb{R}$ :
- le réel $x \in \mathbb{R}$ est un minorant (resp. majorant) de $P$ si et seulement si $x$ est inférieur (resp. supérieur) à tout réel de $P$ ;
- le réel $x \in P$ est un minimum (resp. maximum) de $P$ si et seulement si $x$ est inférieur (resp. supérieur) à tout réel de $P$ ;
- le réel $x \in \mathbb{R}$ est l'infimum (resp. supremum) de $P$ si et seulement si $x$ est le maximum (resp. minimum) de l'ensemble des minorants (resp. majorants) de $P$ ;
- $P$ est une partie minorée (resp. partie majorée) de $(\mathbb{R}, \leq)$ si et seulement si l'ensemble des minorants (resp. majorants) de $P$ n'est pas vide ;
- $P$ est une partie bornée de $(\mathbb{R}, \leq)$ si et seulement si $P$ est une partie majorée et minorée de $(\mathbb{R}, \leq)$.