UKOnline

Algèbre linéaire

Terminons ce chapitre avec plusieurs problèmes d'algèbre linéaire qu'il est possible de résoudre à l'aide de matrices et de fonctions de l'écosystème SciPy. On va aborder la résolution de systèmes d'équations linéaires, l'utilisation de valeurs et vecteurs propres et la décomposition de matrices. Enfin, on termine cette section, et ce chapitre, en examinant brièvement quelques considérations sur les performances.

Systèmes d'équations linéaires

Le premier type de problème qui nous intéresse est la résolution d'un système d'équations linéaires. Pour rappel, il s'agit d'un système de $m$ équations qui portent sur les mêmes $n$ inconnues. On peut écrire un tel système, de manière générale, comme suit :

$$\left\{ \begin{array}{*{7}{c}} a_{11} x_1 & + & \dots & + & a_{1n} x_n & = & b_1 \\ \vdots & & \ddots & & \vdots & = & \vdots \\ a_{m1} x_1 & + & \dots & + & a_{mn} x_n & = & b_m \\ \end{array} \right.$$

Il y a en tout $m \times n$ coefficients ($a_{ij}$), $n$ variables ($x_j$) et $m$ termes indépendants ($b_i$). Ce système d'équations linéaires peut s'écrire de manière plus compacte, par l'équation matricielle $Ax = b$, avec les définitions de matrices suivantes :

$$A = \left( \begin{array}{ccc} a_{11} & \dots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \dots & a_{mn} \end{array} \right), \quad x = \left( \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right), \quad b = \left( \begin{array}{c} b_1 \\ \vdots \\ b_n \end{array} \right).$$

Résolution exacte

Résoudre un système d'équations linéaires revient à trouver les valeurs des $n$ variables $x_j$, telles que les $m$ équations soient satisfaites. En multipliant les deux membres de l'équation matricielle par $A^{-1}$, à gauche, on déduit que la solution est simplement $x = A^{-1}b$. C'est donc assez facile de résoudre un système d'équations linéaires avec NumPy, à partir d'une description de ce dernier par les matrices $A$ et $b$. L'exemple suivant résout un tel système :

A = np.matrix('1 2;3 4') b = np.matrix('1;0') x = A.I * b print(x)

La solution à ce système est unique et s'obtient assez facilement à la main, en isolant l'une des variables dans l'une des équations pour ensuite injecter sa valeur dans l'autre équation. Finalement, on trouve :

$$\left\{ \begin{array}{*{5}{c}} x_1 & + & 2x_2 & = & 1 \\ 3x_1 & + & 4x_2 & = & 0 \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{rcl} x_1 & = & -2 \\ x_2 & = & 1,\!5 \\ \end{array} \right.$$

L'exécution du programme donne le même résultat pour x, sous la forme d'une matrice de dimensions $2 \times 1$, c'est-à-dire :

[[-2. ]
 [ 1.5]]

Résoudre le système en calculant la valeur de A.I * b fonctionne lorsque l'on a des objets de type matrix. De manière générale, si on a des objets ndarray, on peut passer par la fonction inv du module scipy.linalg pour calculer l'inverse et par la méthode dot des tableaux pour calculer le produit matriciel. On peut également directement utiliser la fonction solve du même module, qui offre un raccourci d'écriture. On aurait donc pu être plus général en écrivant :

x = inv(A).dot(b) x = solve(A, b)

La technique de résolution exacte que l'on vient de décrire ne fonctionne que lorsque l'inverse de $A$ existe. On ne peut donc l'utiliser que lorsque l'on est sûr qu'une solution existe pour le système d'équations linéaires.

Approximation

Tous les systèmes d'équations linéaires ne peuvent pas être résolus. Si la matrice $A$ est singulière, et donc non-inversible, le système n'admet pas de solution. Prenons l'exemple suivant :

A = np.matrix('1 2;2 4') b = np.matrix('1;0') x = A.I * b print(x)

Son exécution provoque immédiatement une erreur d'exécution lorsque l'on tente d'inverser la matrice $A$, indiquant dans le message d'erreur que la matrice est singulière :

Traceback (most recent call last):
  File "program.py", line 6, in <module>
    print(A.I * b)
  File "/usr/local/lib/python3.7/site-packages/numpy/matrixlib/defmatrix.py", line 831, in getI
    return asmatrix(func(self))
  File "/usr/local/lib/python3.7/site-packages/numpy/linalg/linalg.py", line 532, in inv
    ainv = _umath_linalg.inv(a, signature=signature, extobj=extobj)
  File "/usr/local/lib/python3.7/site-packages/numpy/linalg/linalg.py", line 89, in _raise_linalgerror_singular
    raise LinAlgError("Singular matrix")
numpy.linalg.linalg.LinAlgError: Singular matrix

Heureusement, tout n'est pas perdu. On peut, en effet, obtenir une solution approximative, qui va faire en sorte que $Ax$ soit le plus proche possible de $b$, c'est-à-dire une solution qui va minimiser $b - Ax$. Pour cela, il suffit d'utiliser la fonction lstsq du module scipy.linalg, à qui on passe en paramètres les matrices $A$ et $b$, comme ci-dessous :

print(lstsq(A, b))

Suite à son exécution, la fonction renvoie un tuple avec la solution approximée comme premier élément, c'est-à-dire $x_1 = 0,\!04$ et $x_2 = 0,\!08$ dans notre cas, comme on le voit ci-dessous :

(array([[0.04],
       [0.08]]), array([], dtype=float64), 1, array([5.00000000e+00, 1.98602732e-16]))

Que se passe-t-il si l'on doit résoudre un système d'équations linéaires qui a moins d'équations qu'il n'a d'inconnues. Un tel système possède plusieurs degrés de libertés et admet ainsi plusieurs solutions possibles.

Prenons, par exemple, le système d'équations linéaires constitué d'une seule équation linéaire $\left\{ x_1 + x_2 = 2 \right.$. Une solution possible pour ce système est $x_1 = 1$ et $x_2 = 1$. Mais on pourrait également avoir $x_1 = 3$ et $x_2 = -1$ comme solution. Que se passe-t-il si on résout ce système comme on l'a vu plus haut :

A = np.matrix('1 1') b = np.matrix('2') x = A.I * b print(x)

On va, en fait, obtenir une des solutions acceptables pour le système :

[[1.]
 [1.]]

On verra plus loin, au chapitre 6, comment il est possible d'obtenir une description de toutes les solutions possibles, lorsqu'il en existe plusieurs, à l'aide de la librairie SymPy.

Valeur et vecteur propre

Le deuxième type de problème que l'on peut vouloir résoudre consiste à retrouver les valeurs et vecteurs propres d'une matrice. Ces deux éléments jouent un rôle dans beaucoup de problèmes, comme pour décomposer une matrice afin d'accélérer certaines opérations, ou encore pour trouver quelle page web est la plus populaire sur internet.

Pour rappel, pour une matrice carrée $A$ d'ordre $n$, le scalaire $\lambda$ est une valeur propre de cette matrice s'il existe un vecteur $x$, non-nul et de longueur $n$, tel que l'équation suivante soit satisfaite :

$$Ax = \lambda x.$$

Multiplier la matrice $A$ par ce vecteur $x$ revient donc simplement à multiplier le vecteur $x$ par le scalaire $\lambda$. Ce vecteur $x$ est appelé vecteur propre de $A$ associé à la valeur propre $\lambda$. Un même vecteur propre ne peut d'ailleurs pas être associé à des valeurs propres différentes.

Application linéaire

On peut comprendre plus intuitivement les notions de valeurs et vecteurs propres en s'intéressant au concept d'application linéaire. Sans rentrer dans les détails, il s'agit de réaliser une transformation des vecteurs d'un espace donné, de sorte que l'addition et la colinéarité soient préservés après transformation.

Par exemple, dans le plan, des transformations géométriques, telles que la symétrie d'axe $x$ ou une rotation de centre $(0, 0)$, sont des applications linéaires. On peut représenter une telle transformation à l'aide d'une matrice, par laquelle il suffit de multiplier les vecteurs pour les transformer. Prenons comme simple exemple une mise à l'échelle verticale dans le plan, d'un facteur $1/2$. La figure 3 montre un triangle avant et après transformation.

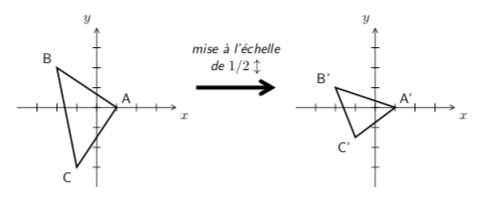
Pour réaliser la mise à l'échelle, on va représenter chaque point du triangle par un vecteur avec deux composantes, ses coordonnées en $x$ et en $y$. Les trois points $A$, $B$ et $C$ du triangle sont donc, respectivement, représentés par les vecteurs $(1, 0)$, $(-2, 2)$ et $(-1, -3)$. La matrice qui représente la mise à l'échelle verticale d'un facteur $1/2$ est la suivante :

$$T = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1/2 \end{array} \right).$$

On obtient les points $A'$, $B'$ et $C'$ du triangle transformé en multipliant la matrice $T$ par les vecteurs représentant chacun des points du triangle :

$$A' = TA = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1/2 \end{array} \right) \left( \begin{array}{c} 1 \\ 0 \end{array} \right) = \left( \begin{array}{c} 1 \\ 0 \end{array} \right),$$ $$B' = TB = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1/2 \end{array} \right) \left( \begin{array}{c} -2 \\ 2 \end{array} \right) = \left( \begin{array}{c} -2 \\ 1 \end{array} \right),$$ $$C' = TC = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1/2 \end{array} \right) \left( \begin{array}{c} -1 \\ -3 \end{array} \right) = \left( \begin{array}{c} -1 \\ -3/2 \end{array} \right).$$

On obtient exactement les mêmes résultats avec les instructions suivantes, où on a transposé les matrices représentant les points du triangle pour pouvoir appliquer la multiplication matricielle :

T = np.matrix('1 0;0 0.5') triangle = [ np.matrix('1 0'), np.matrix('-2 2'), np.matrix('-1 -3') ] for p in triangle: print(T * p.T)

Chacun des points du triangle subit donc la transformation, de par la multiplication matricielle par $T$ que l'on applique, pour donner le même résultat que celui calculé plus haut :

[[1.]
 [0.]]
[[-2.]
 [ 1.]]
[[-1. ]
 [-1.5]]

Interprétation géométrique

Intuitivement, un vecteur propre est un vecteur qui garde la même direction après avoir subi une transformation linéaire. Par contre, il pourrait très bien avoir changé de longueur, voire de sens. Le facteur de multiplication subi par le vecteur est en fait donné par la valeur propre associée au vecteur propre.

Pour cet exemple de transformation, les deux vecteurs propres sont $(1, 0)$ et $(0, 1)$. Si on applique la transformation dessus, en les pré-multipliant par $T$, on obtient les vecteurs transformés suivants :

$$\left( \begin{array}{cc} 1 & 0 \\ 0 & 1/2 \end{array} \right) \left( \begin{array}{c} 1 \\ 0 \end{array} \right) = \left( \begin{array}{c} 1 \\ 0 \end{array} \right) \textrm{ et } \left( \begin{array}{cc} 1 & 0 \\ 0 & 1/2 \end{array} \right) \left( \begin{array}{c} 0 \\ 1 \end{array} \right) = \left( \begin{array}{c} 0 \\ 1/2 \end{array} \right).$$

Pour le premier vecteur propre, on voit qu'il reste le même après transformation, la valeur propre associée est donc de $1$, et pour le second, il a été compressé d'un facteur $1/2$ et la valeur propre associé est donc $1/2$.

Fonction eig

Pour obtenir les valeurs et vecteurs propres d'une matrice carrée, on utilise la fonction eig du module scipy.linalg. Cette dernière renvoie un tuple les contenant, comme le montre l'exemple suivant :

eigval, eigvec = eig(T) print(eigval) print(eigvec)

Le premier élément du tuple contient un tableau avec les valeurs propres, sous forme de nombres complexes, et le second élément du tuple contient un tableau avec les vecteurs propres associés. Le résultat de l'exécution confirme les résultats présentés plus haut :

[1. +0.j 0.5+0.j]
[[1. 0.]
 [0. 1.]]

Le vecteur propre associé à la valeur propre eigval[i] est la $i$^e colonne du tableau eigvec, à savoir le vecteur eigvec[:,i]. La valeur propre $1$ est donc associée au vecteur propre $(1, 0)^t$ et la valeur propre $1/2$ est associée au vecteur propre $(0, 1)^t$. Les vecteurs propres renvoyés par la fonction eig sont également normalisés, c'est-à-dire qu'ils sont tel que leur norme est ramenée à $1$.

On peut vérifier l'interprétation géométrique expliquée plus haut, en comparant le vecteur propre transformé par la matrice $T$ avec la multiplication du vecteur propre par la valeur propre qui lui est associée, c'est-à-dire faire le calcul $Tx = \lambda x$ pour chacun des $x$ :

for i in range(len(eigvec)): v = eigvec[:,i] print(np.allclose(T @ v, eigval[i] * v))

Comme on est avec du calcul en nombres flottants, et même en nombres complexes en fait, on a utilisé la fonction allclose déjà introduite plus haut en section 3.3.5 pour faire la comparaison. Sans surprise, on obtient deux True suite à l'exécution de ces instructions, l'interprétation géométrique étant ainsi vérifiée :

True
True

Notez que si l'on n'est intéressé que par les valeurs propres, on peut plutôt utiliser la fonction eigvals, toujours du module scipy.linalg, pour n'obtenir que les valeurs propres d'une matrice donnée.

Décomposition de matrice

On a vu, dans la section précédente, que l'on pouvait représenter un système d'équations linéaires par une matrice $A$ et une matrice $b$. Pour résoudre le système, il suffit essentiellement d'inverser la matrice $A$, ce qui peut d'ailleurs couter assez cher en temps de calcul. En réalité, on peut tirer pleins d'autres propriétés intéressantes sur le système et ses solutions en analysant cette matrice $A$. Il est donc assez important d'être capable de faire des opérations de manière efficace sur cette dernière.

Diagonalisation

Si une matrice carrée $A$ d'ordre $n$ possède exactement $n$ vecteurs propres indépendants, on peut la diagonaliser, c'est-à-dire l'écrire sous la forme suivante, où $P$ et $D$ sont des matrices carrées d'ordre $n$ et où $D$ est en plus une matrice diagonale :

$$A = P D P^{-1}.$$

On construit la matrice $P$ en y plaçant simplement les vecteurs propres de $A$ et la matrice $D$ est une matrice diagonale constituée avec les valeurs propres de $A$. Voyons un exemple qui illustre cette décomposition :

A = np.matrix('2 1;1 2') eigval, eigvec = eig(A) P = np.mat(eigvec) D = np.diag(eigval) print(P * D * P.I)

Ce programme déclare une matrice $A$ et en calcule les valeurs et les vecteurs propres à l'aide de la fonction eig. Il construit ensuite les deux matrices $P$ et $D$ et calcule le résultat du produit $PDP^{-1}$. Le résultat de l'exécution montre que l'on retrouve ainsi la matrice $A$ :

[[2.+0.j 1.+0.j]
 [1.+0.j 2.+0.j]]

On a donc réussi à décomposer la matrice $A$ en un produit de trois matrices, plus simples que $A$ :

$$A = \left( \begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right) = \left( \begin{array}{cc} 0,\!7 & -0,\!7 \\ 0,\!7 & 0,\!7 \end{array} \right) \left( \begin{array}{cc} 3 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{cc} 0,\!7 & 0,\!7 \\ -0,\!7 & 0,\!7 \end{array} \right).$$

L'un des intérêts de la diagonalisation est qu'elle permet de calculer des puissances de matrices de manière très efficace. On peut en effet se baser sur la propriété suivante :

$$A^k = (PDP^{-1})^k = PD^kP^{-1},$$

sachant qu'élever une matrice diagonale à la puissance $k$ revient à élever chacun des éléments de sa diagonale par $k$. Pour calculer la $k$^e puissance de la matrice $A$, cela prend en moyenne 0,025ms si on choisit $k = 50$, alors qu'il ne faut que 0,008ms pour obtenir le même résultat à partir de la forme diagonalisée de $A$, soit une amélioration de $68\%$.

Pour être précis, il faudrait prendre en compte le temps nécessaire à la diagonalisation en tant que telle, mais c'est une opération qu'il ne faut faire qu'une seule fois. Il s'agit donc d'investir un peu de temps de calcul pour ensuite accélérer l'exécution des calculs futurs.

Autre décomposition

Il existe beaucoup d'autres décompositions de matrice possibles, toutes supportées pas des fonctions du module scipy.linalg, mais on ne va pas les détailler dans le cadre de ce cours. Juste pour les citer, il y a la décomposition $LU$ (lu ou lu_factor), de Choleski (choleski), la décomposition $QR$ (qr), la décomposition en valeurs singulières (svd) et encore quelques autres moins connues que vous trouverez dans la documentation du module scipy.linalg.

La décomposition en valeurs singulières (SVD) est assez intéressante, car elle permet de résoudre un problème très concret, à savoir celui de la compression d'images. Une matrice $A$, rectangulaire de dimensions $m \times n$, peut se réécrire sous la forme suivante :

$$A = U \Sigma V^*,$$

où $U$ est une matrice unitaire carrée d'ordre $m$, $\Sigma$ est une matrice rectangulaire diagonale de dimensions $m \times n$ et $V$ est une matrice unitaire carrée d'ordre $n$. Pour rappel, $V^*$ représente la matrice adjointe de $V$, c'est-à-dire la transposée de la matrice conjuguée de $V$. Les éléments de la diagonale de $\Sigma$ sont les valeurs singulières de $A$.

Pour compresser une image, représentée par une matrice, une solution consiste à la décomposer en valeurs singulières et, d'ensuite, sélectionner un sous-ensemble de ses valeurs singulières. On obtient ainsi une sous-matrice de $\Sigma$ et, en réduisant également $U$ et $V^*$ en conséquence, on peut recalculer une nouvelle image $A' = U'\Sigma'V'^*$, qui occupe moins de place que $A$. On reviendra sur cette application au chapitre 4, avec une démonstration du résultat obtenu par cette technique de compression.

Performance

Terminons ce chapitre sur les matrices et le calcul matriciel par quelques éléments importants en lien avec la performance des calculs et avec les possibilités de faire plusieurs opérations en une fois.

Représentation de matrice

On a vu, dans ce chapitre, que NumPy définit une sous-classe de ndarray pour le cas particulier des matrices, à savoir la classe matrix. On a également vu que les opérations, notamment la multiplication, ne se comportent pas de la même manière selon le type des opérandes.

Le tableau de la figure 4 reprend les différents opérateurs et fonctions et résume ce qu'ils calculent. Après, il y a d'autres différences plus subtiles qu'il faut éclaircir en se référant à la documentation. Par exemple, les fonctions matmul et dot font une multiplication matricielle sur des ndarray, sauf que la seconde est plus générale et peut notamment faire du broadcasting.

Si l'on se réfère à la documentation de NumPy, il n'est pas recommandé d'utiliser la classe matrix, mais de tout faire avec des ndarray. Les opérateurs et les fonctions existent pour les deux, et n'utiliser que des ndarray rend le code plus lisible et évite de faire, ou de devoir penser à faire, des conversions à tout moment pour que les opérations réalisées soit les bonnes. On peut même lire, dans la documentation, que la classe matrix pourrait être supprimée dans des versions futures de la librairie NumPy et qu'il vaut mieux limiter son utilisation au strict minimum.

Opérateur/Fonction	ndarray	matrix
*	par élément	matriciel
@	matriciel	matriciel
multiply	par élément	par élément
matmul	matriciel	matriciel
dot	par élément ou matriciel	par élément ou matriciel

Pour résumer, il est préférable de toujours utiliser des ndarray, et d'utiliser l'opérateur * pour réaliser un produit par élément et @ pour un matriciel, lorsque l'on fait du calcul matriciel. De manière plus générale, on passera par les fonctions multiply ou matmul selon le produit que l'on désire. On tâchera de ne pas trop utiliser la fonction dot, car son comportement dépend des paramètres qui lui sont passés.

Modules linalg

Le deuxième élément intéressant à observer est qu'il existe deux modules d'algèbre linéaire dans l'écosystème SciPy. En effet, on a déjà pu se rendre compte qu'il existe le module scipy.linalg et le module numpy.linalg. La plupart des fonctions se retrouvent dans les deux modules et fonctionnent exactement de la même manière.

On peut néanmoins relever des différences entre les deux modules. La première est que le module scipy.linalg est toujours compilé avec ATLAS LAPACK et BLAS, deux librairies optimisées et de bas niveau qui permettent de faire des opérations d'algèbre linéaire de manière très efficace. Le module numpy.linalg, quant à lui, se veut plus portable afin de pouvoir être installé plus facilement sur n'importe quelle machine, et fera donc certaines opérations en pur Python plutôt que de dépendre de librairies tierces optimisées.

Certaines fonctions n'existent que dans le module numpy.linalg, comme matrix_rank ou matrix_power, par exemple, qui sont respectivement utilisées pour calculer le rang d'une matrice ou élever une matrice à une certaine puissance. La raison est simplement que ces opérations ne sont pas supportées par LAPACK ou BLAS.

La bonne pratique consiste à d'abord utiliser les fonctions de scipy.linalg si possible, et de se tourner vers numpy.linalg pour ce qui n'est pas possible autrement.

Calcul multiple

La deuxième différence que l'on peut observer entre les deux modules scipy.linalg et numpy.linalg est que certaines des fonctions du second module peuvent réaliser la même opération sur plusieurs matrices à la fois. Regardons, par exemple, la fonction inv qui permet d'inverser une matrice. Dans les deux modules, cette fonction prend un seul paramètre, mais dans la version du module scipy.linalg, on peut lire qu'il doit s'agir d'une matrice carrée et dans la version du module numpy.linalg, on voit que la description du paramètre est (..., M, M) array_like.

En fait, on va pouvoir empiler plusieurs matrices carrées, en utilisant une dimension supplémentaire. La fonction va ensuite inverser ces différentes matrices, en un seul appel. L'exemple suivant illustre cette possibilité :

A = np.array([[4, 3], [3, 2]]) B = np.array([[-3, 1], [5, -2]]) M = np.array([A, B]) print(inv(M))

Les deux matrices $A$ et $B$ ont été mises dans un même tableau et inversées en un seul appel de fonction qui renvoie les deux résultats en un seul tableau également :

[[[-2.  3.]
  [ 3. -4.]]

 [[-2. -1.]
  [-5. -3.]]]

• Précédent
• Suivant