UKOnline

Flux d'exécution

Enfin, pour conclure ce chapitre, un dernier élément sur lequel il est possible de jouer pour optimiser un code, c'est le flux d'exécution. Il est très important de choisir, voire de développer, le bon algorithme pour le problème à résoudre. Il est également important de connaitre les possibilités offertes par le langage de programmation.

Comme abordé dans le chapitre suivant, l'utilisation d'outils de mesure de performance permet d'identifier des goulots d'étranglement dans des algorithmes, et donc des zones d'optimisation éventuelle.

Tri de liste

Si on prend l'exemple du tri d'une liste de nombres, on peut déjà observer que bien choisir son algorithme a de l'importance. Par exemple, pour trier une liste déjà triée ou presque triée, le tri par insertion sera généralement plus rapide que le tri rapide.

En prenant deux implémentations (on peut, par exemple, trouver des implémentations toutes faites sur le site de Rosetta Code : https://www.rosettacode.org) en place (un algorithme de tri est dit en place lorsqu'il trie les éléments au sein de la même liste, c'est-à-dire sans en construire et renvoyer une nouvelle), et en les exécutant sur la même liste triée de $800$ éléments, on passe de 19 ms avec le tri par insertion à 31 ms avec le tri rapide, soit une augmentation de temps de 39 %. Il faut, en effet, se rappeler que le tri rapide a une complexité temporelle de $\mathcal{O}(n^2)$ dans le pire cas, à comparer à une complexité temporelle de $\mathcal{O}(n)$ dans le meilleur cas pour le tri par insertion.

La deuxième chose à savoir est qu'il ne faut pas forcément toujours ré-implémenter les algorithmes « connus » soi-même. Il est, en effet, possible d'utiliser des fonctions prédéfinies pour réaliser plus efficacement le tri par insertion et le tri rapide :

Sur la même liste de $800$ éléments, on passe de 19 ms à 0,7 ms pour le tri par insertion et de 31 ms à 5 µs pour le tri rapide. On obtient donc respectivement des diminutions de temps de 96 % et 99,98 %.

Cache

Parfois, une même fonction est appelée plusieurs fois dans un même programme, avec exactement les mêmes paramètres, et elle peut s'avérer couteuse à exécuter. Prenons, par exemple, la fonction suivante qui calcule le $n$e nombre de Fibonacci :

Supposons que l'on souhaite calculer le 25e nombre de Fibonacci. Pour cela, on exécute l'appel de fonction fib(25) et la condition du if n'étant pas satisfaite, on se retrouve à devoir exécuter les deux appels fib(24) et fib(23). Chacun de ces deux appels va nécessiter deux nouveaux appels, à savoir fib(23) et fib(22) pour le premier et fib(22) et fib(21) pour le second, et ainsi de suite comme illustré par la figure 2. On se retrouve en fait à exécuter plusieurs fois le même appel, ce qui n'est absolument pas efficace. En effet, il faut 39 ms de temps d'exécution pour calculer le 25e nombre de Fibonacci, une seule fois.

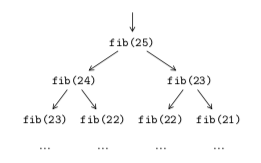
Appels récursifs Fibonacci
Des millions d'appels récursifs sont exécutés suite à l'appel fib(25), lorsque l'on veut calculer le 25e nombre de Fibonacci avec la fonction récursive présentée en bas de la page précédente.

Grâce au décorateur lru_cache du module functools, on va pouvoir sauvegarder les résultats des appels les plus récents pour éviter de devoir les recalculer. Voici comment on peut simplement faire pour stocker le résultat des $128$ appels les plus récents :

Cette fois-ci, pour calculer le 25e nombre de Fibonacci, il ne faut plus que 0,3 µs, soit une diminution de temps de 99,999 %.

Cette technique, connue sous le nom de mémoïsation, consiste à utiliser plus de mémoire pour gagner du temps de calcul, en stockant dans une mémoire cache les résultats d'appels de fonction pour éviter de les exécuter plusieurs fois. Le décorateur lru_cache du module functools permet d'éviter de gérer cette mémoïsation « manuellement ».

Itérateur

Enfin, terminons avec le module itertools qui contient toute une série de fonctions qui permettent de construire des itérateurs divers et variés, à directement utiliser comme blocs de base dans des algorithmes. On y retrouve, par exemple, la fonction product qui permet de calculer le produit cartésien de deux collections. Voici deux fonctions qui permettent de calculer ce produit :

La seconde fonction est plus rapide que la première. En effet, on passe de 193 ms à 134 ms pour calculer le produit cartésien de deux listes de 1000 éléments, soit une diminution de temps de 31 %.