UKOnline

Fonction

Une relation $R$ est une correspondance entre les éléments de deux ensembles $A$ et $B$ :

$$R : A \times B.$$

Les éléments de l'ensemble $A$ qui ont un correspondant dans $B$ sont les antécédents et ceux de l'ensemble $B$ qui ont un correspondant dans $A$ sont les images.

Une fonction $f$ est une relation pour laquelle chaque antécédent n'a qu'une seule image, c'est-à-dire que chaque élément du premier ensemble a au plus une image. Le domaine d'une fonction, noté $\textrm{dom}~f$, est l'ensemble des antécédents. On s'intéresse aux fonctions réelles à une variable, que l'on désignera habituellement par $x$. On définit classiquement une fonction en associant à chaque valeur $x$ de son domaine, l'image correspondante $f(x)$, ce qu'on notera :

$$f : \begin{array}[t]{rcl} D & \rightarrow & B \\ x & \mapsto & f(x), \end{array}$$

où $D \subseteq \mathbb{R}$ et $B \subseteq \mathbb{R}$.

Voici plusieurs propriétés permettant de caractériser une fonction. On peut spécifier ces différentes caractéristiques sur le domaine complet, ou sur un intervalle $I$ de ce dernier.

1. Une fonction est (strictement) croissante, si lorsque $x_1 < x_2$, alors $f(x_1) \leq f(x_2)$ ($f(x_1) < f(x_2)$).
2. Une fonction est (strictement) décroissante, si lorsque $x_1 > x_2$, alors $f(x_1) \geq f(x_2)$ ($f(x_1) > f(x_2)$).
3. Le réel $a \in D$ est une racine d'une fonction, si son image par la fonction vaut $0$.
4. Une fonction est paire si $f(x) = f(-x)$ pour tout point $x \in D$; son graphe admet une symétrie d'axe $y$.
5. Une fonction est impaire si $f(-x) = -f(x)$ pour tout point $x \in D$; son graphe admet une symétrie dont le centre est l'origine du repère.
6. Une fonction admet un maximum (resp. minimum) en un point $a \in D$ lorsqu'elle cesse de croitre (resp. décroitre) en $a$ pour commencer à décroitre (resp. croitre).
7. Une fonction est périodique de période $p$ non nulle si $f(x + p) = f(x)$ pour tout point $x \in D$.

Fonction usuelle

Cette section reprend plusieurs fonctions usuelles, avec leur nom, leur équation, le graphe correspondant et quelques caractéristiques. Lorsqu'utilisée, la valeur $k$ est à considérer comme un entier ($k \in \mathbb{Z}$).

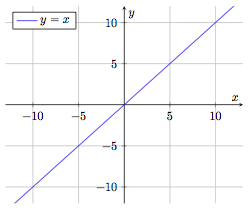	Fonction identité $$f : \begin{array}[t]{rcl} \mathbb{R} & \rightarrow & \mathbb{R} \\ x & \mapsto & f(x) = x \end{array}$$ Strictement croissante Racine en $x = 0$ Impaire
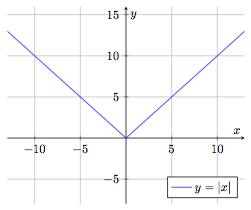	Fonction valeur absolue $$f : \begin{array}[t]{rcl} \mathbb{R} & \rightarrow & \mathbb{R}^+ \\ x & \mapsto & f(x) = |x| \end{array}$$ Paire Racine en $x = 0$ Minimum en $x = 0$
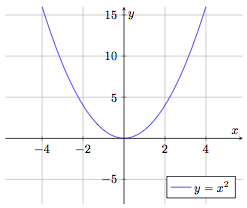	Fonction carré $$f : \begin{array}[t]{rcl} \mathbb{R} & \rightarrow & \mathbb{R}^+ \\ x & \mapsto & f(x) = x^2 \end{array}$$ Paire Racine en $x = 0$ Minimum en $x = 0$
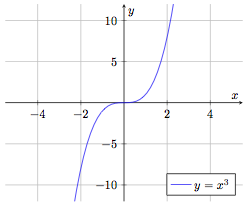	Fonction cube $$f : \begin{array}[t]{rcl} \mathbb{R} & \rightarrow & \mathbb{R} \\ x & \mapsto & f(x) = x^3 \end{array}$$ Strictement croissante Impaire Racine en $x = 0$
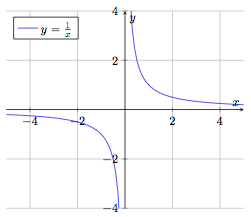	Fonction inverse $$f : \begin{array}[t]{rcl} \mathbb{R}_0 & \rightarrow & \mathbb{R} \\ x & \mapsto & f(x) = \frac{1}{x} \end{array}$$ Impaire
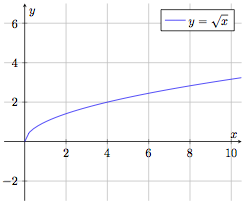	Fonction racine carrée $$f : \begin{array}[t]{rcl} \mathbb{R}^+ & \rightarrow & \mathbb{R}^+ \\ x & \mapsto & f(x) = \sqrt{x} \end{array}$$ Strictement croissante Racine en $x = 0$ Minimum en $x = 0$
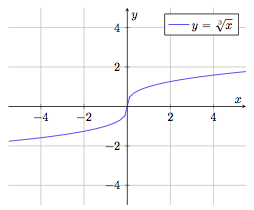	Fonction racine cubique $$f : \begin{array}[t]{rcl} \mathbb{R} & \rightarrow & \mathbb{R} \\ x & \mapsto & f(x) = \sqrt[3]{x} \end{array}$$ Strictement croissante Racine en $x = 0$ Impaire
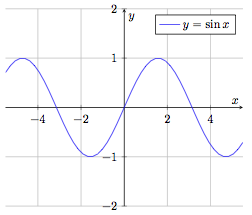	Fonction sinus $$f : \begin{array}[t]{rcl} \mathbb{R} & \rightarrow & [-1, 1] \\ x & \mapsto & f(x) = \sin x \end{array}$$ Racine en $x = k\pi$ Impaire Maximum en $x = \frac{\pi}{2} + 2k\pi$ Minimum en $x = -\frac{\pi}{2} + 2k\pi$ Périodique de période $2\pi$
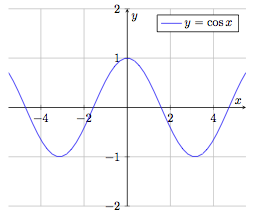	Fonction cosinus $$f : \begin{array}[t]{rcl} \mathbb{R} & \rightarrow & [-1, 1] \\ x & \mapsto & f(x) = \cos x \end{array}$$ Racine en $\frac{\pi}{2} + k\pi$ Paire Maximum en $x = 2k\pi$ Minimum en $x = \pi + 2k\pi$ Périodique de période $2\pi$
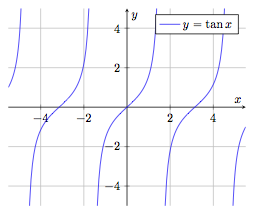	Fonction cosinus $$f : \begin{array}[t]{rcl} \mathbb{R} \setminus \left\{ \frac{\pi}{2} + k\pi \right\} & \rightarrow & \mathbb{R} \\ x & \mapsto & f(x) = \tan x \end{array}$$ Racine en $x = k\pi$ Impaire Périodique de période $\pi$
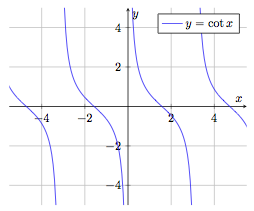	Fonction cotangente $$f : \begin{array}[t]{rcl} \mathbb{R} \setminus \left\{ k\pi \right\} & \rightarrow & \mathbb{R} \\ x & \mapsto & f(x) = \cot x \end{array}$$ Racine en $x = \frac{\pi}{2} + k\pi$ Impaire Périodique de période $\pi$
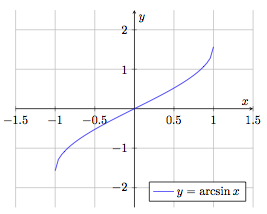	Fonction arcsinus $$f : \begin{array}[t]{rcl} [-1, 1] & \rightarrow & \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \\[1mm] x & \mapsto & f(x) = \arcsin x \end{array}$$ Strictement croissante Racine en $x = 0$ Impaire Maximum en $x = 1$ Minimum en $x = -1$
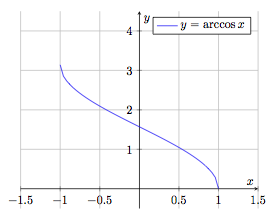	Fonction arccosinus $$f : \begin{array}[t]{rcl} [-1, 1] & \rightarrow & \left[ 0, \pi \right] \\[1mm] x & \mapsto & f(x) = \arccos x \end{array}$$ Strictement décroissante Racine en $x = 1$ Maximum en $x = -1$ Minimum en $x = 1$
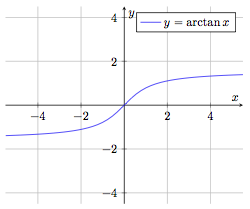	Fonction arctangente $$f : \begin{array}[t]{rcl} \mathbb{R} & \rightarrow & \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \\[1mm] x & \mapsto & f(x) = \arctan x \end{array}$$ Strictement croissante Racine en $x = 0$ Impaire
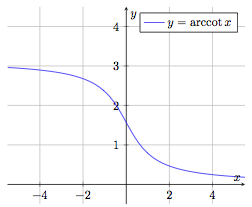	Fonction arccotangente $$f : \begin{array}[t]{rcl} \mathbb{R} & \rightarrow & \left[ 0, \pi \right] \\[1mm] x & \mapsto & f(x) = \textrm{arccot}\: x \end{array}$$ Strictement décroissante
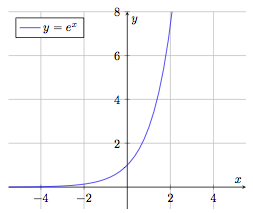	Fonction exponentielle $$f : \begin{array}[t]{rcl} \mathbb{R} & \rightarrow & \mathbb{R}_0^+ \\ x & \mapsto & f(x) = e^x \end{array}$$ Strictement croissante
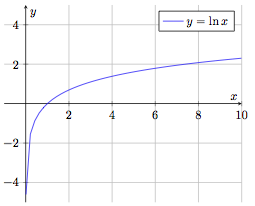	Fonction logarithme $$f : \begin{array}[t]{rcl} \mathbb{R}_0^+ & \rightarrow & \mathbb{R} \\ x & \mapsto & f(x) = \ln x \end{array}$$ Strictement croissante Racine en $x = e$

Fonction associée

Étant donnée une fonction $f(x)$, on peut construire une nouvelle fonction, appelée fonction associée, dont on obtient le graphe (et donc les images des points du domaine) par manipulation du graphe de $f(x)$ :

1. $g(x) = f(x) + k$ ajoute $k$ à toutes les ordonnées ;
2. $g(x) = kf(x)$ multiplie toutes les ordonnées par $k$ ;
3. $g(x) = f(x + k)$ soustrait $k$ à toutes les abscisses ;
4. $g(x) = f(kx)$ divise toutes les abscisses par $k$ ;
5. et enfin $g(x) = |f(x)|$ conserve la partie du graphe située au-dessus de l'axe des $x$, et remplace la partie se situant en dessous par sa symétrie d'axe $x$.

• Précédent
• Suivant