Arc
Commençons avec quelques propriétés de base liant les amplitudes des angles et des arcs qu'ils interceptent. Pour rappel, un angle est inscrit dans un cercle si son sommet se trouve sur le cercle.
-
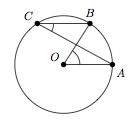
Dans tout cercle, des angles au centre de même amplitude interceptent des arcs de même longueur et inversement :
$$\widehat{AOB} = \widehat{COD} \iff \stackrel\frown{AB} = \:\stackrel\frown{CD}.$$
-
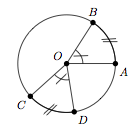
Dans tout cercle, l'amplitude d'un angle au centre $\widehat{AOB}$ est double de celle de l'angle inscrit $\widehat{ACB}$ interceptant le même arc $\stackrel\frown{AB}$ :
$$\widehat{AOB} = 2\widehat{ACB}.$$
-
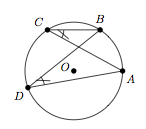
Dans tout cercle, deux angles inscrits $\widehat{ACB}$ et $\widehat{ADB}$ qui interceptent le même arc $\stackrel\frown{AB}$ ont la même amplitude :
$$\widehat{ACB} = \widehat{ADB}.$$
Voici maintenant trois autres propriétés qui font intervenir plusieurs types d'angle dans un cercle :
-
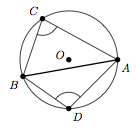
Dans tout cercle, la somme des amplitudes de deux angles inscrits interceptant la même corde et situés de part et d'autre de cette corde vaut $180^\circ$.
$$\widehat{ACB} + \widehat{ADB} = 180^\circ.$$
-
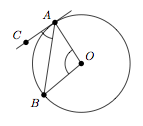
Dans tout cercle, l'amplitude d'un angle au centre vaut le double de l'angle tangentiel interceptant le même arc.
$$\widehat{AOB} = 2\widehat{BAC}.$$
-
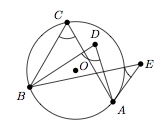
Dans tout cercle, l'amplitude d'un angle dont le sommet est intérieur (resp. extérieur) au cercle est plus grande (resp. petite) que l'amplitude de l'angle inscrit interceptant le même arc.
$$\widehat{ADB} > \widehat{ACB} \textrm{ et } \widehat{AEB} < \widehat{ACB}.$$
Arc capable d'un angle
Un arc capable d'un angle $\alpha$ construit à partir d'un segment $[AB]$ est le lieu des points d'où le segment $[AB]$ est vu avec l'angle $\alpha$. Ce lieu est symétrique par rapport à la droite $AB$.
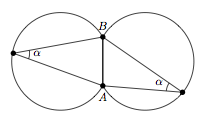
Ce lieu est constitué de deux arcs de cercles sous-tendus par la corde $[AB]$ et symétriques par rapport à la droite $AB$, à l'exception des points $A$ et $B$.
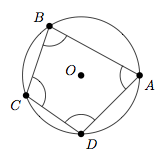
Quadrilatère inscrit dans un cercle
Un quadrilatère est convexe s'il se trouve à chaque fois dans un même demi-plan par rapport à chaque droite définie par chacun de ses côtés.
Si un quadrilatère convexe est inscrit à un cercle, la somme de deux angles opposés est égale à $180^\circ$, et inversement.
La figure suivante montre un quadrilatère convexe, on a :
$$\begin{array}{l} ABCD \textrm{ est inscrit dans le cercle} \\[1mm] \hspace{2cm} \iff \widehat{ABC} + \widehat{CDA} = 180^\circ \textrm{ et } \widehat{DAB} + \widehat{BCD} = 180^\circ. \end{array}$$